Recientemente, se generó un debate en torno a la pregunta 61 de la PAES de Matemáticas M1, que fue considerada por académicos y profesores de preuniversitarios como una de las más difíciles. Esta pregunta, que implicaba calcular el volumen de un perfil rectangular hueco de aluminio con medidas específicas, causó controversia debido a su redacción, que muchos interpretaron como confusa.
El Planteamiento del Problema
La pregunta solicitaba determinar el volumen de un perfil rectangular de aluminio que tiene un grosor de 4.8 mm y dimensiones de 50.8 mm de altura y 101.6 mm de largo. A simple vista, el problema parece sencillo, pero su complejidad radica en que, para calcular el volumen del material, los estudiantes debían restar el volumen del hueco interno del perfil.
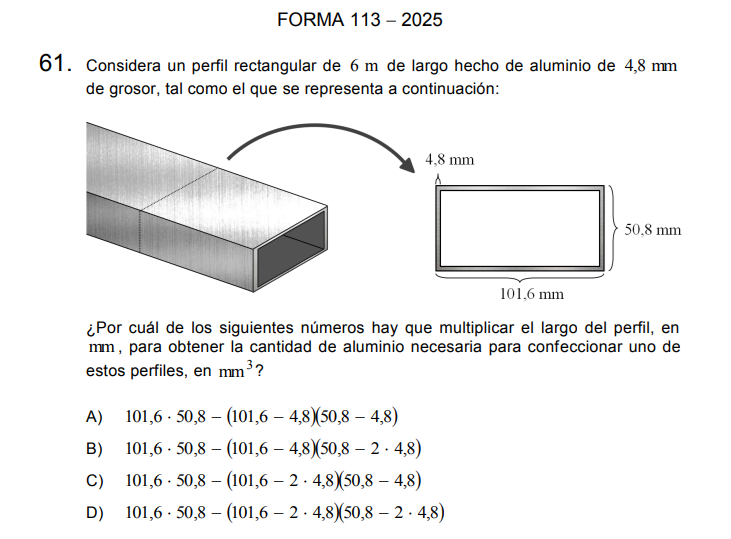
El enunciado pedía a los estudiantes que identificaran cuál de las siguientes expresiones era la correcta para calcular el volumen del material necesario para confeccionar el perfil. Las opciones presentadas (A, B, C, D) correspondían a distintas fórmulas que combinaban las dimensiones dadas, y era necesario aplicar el razonamiento matemático adecuado para elegir la correcta.
La Dificultad en la Redacción y su Impacto en los Estudiantes
Según Mario Ponce, presidente de la Sociedad de Matemática de Chile, el problema es complejo no solo por su contenido, sino también por la redacción que dificulta la interpretación del enunciado. Los términos utilizados en la pregunta no eran del todo familiares para los estudiantes, lo que llevó a confusión al momento de abordar el problema.
«Este tipo de problemas requiere un razonamiento abstracto, que no es común en las pruebas estándar. Los estudiantes deben entender cómo aplicar las fórmulas de volumen de una manera que no se les presenta habitualmente en los ejercicios previos», comenta Ponce. Este tipo de planteamiento, aunque está alineado con los objetivos de la prueba, resultó ser un desafío para aquellos estudiantes que no están acostumbrados a este tipo de problemas.
El Razonamiento Matemático Requerido
El problema tiene una finalidad clara: evaluar la capacidad de los estudiantes para razonar y modelar situaciones matemáticas complejas. El concepto clave detrás de este ejercicio es el de la diferencia de volúmenes, que requiere restar el volumen del hueco interno al volumen total del perfil. Esta habilidad de modelar y razonar sobre problemas abstractos es uno de los objetivos de la PAES, pero también es uno de los más difíciles de lograr para los estudiantes de enseñanza media.
El cálculo del volumen debe realizarse considerando las dimensiones exteriores del perfil y el grosor del material. A partir de esta comprensión, los estudiantes deben identificar la fórmula correcta que permita calcular el volumen de aluminio necesario para construir dicho perfil.
La Solución: ¿Por Qué la Alternativa D es la Correcta?
La solución correcta, según los expertos, es la alternativa D, que presenta la expresión adecuada para calcular el volumen del aluminio necesario. Este tipo de problemas no solo mide la capacidad de los estudiantes para aplicar fórmulas, sino también su habilidad para interpretar y resolver problemas complejos, algo que no siempre se trabaja de manera directa en las clases tradicionales.
Reflexión sobre la Enseñanza de las Matemáticas
Este tipo de preguntas, aunque difíciles, son una oportunidad para repensar cómo enseñamos matemáticas en Chile. Si bien la PAES busca evaluar habilidades matemáticas avanzadas, es fundamental que los estudiantes estén preparados para este tipo de razonamiento abstracto. La habilidad para resolver problemas complejos requiere de una formación sólida en el pensamiento matemático, que combine teoría y práctica de manera efectiva.
En este sentido, es clave que los profesores de matemáticas trabajen en el aula no solo la memorización de fórmulas, sino también la capacidad de los estudiantes para interpretar y modelar problemas matemáticos. La enseñanza de las matemáticas debe ir más allá de los ejercicios tradicionales y fomentar la reflexión profunda sobre los conceptos, preparando a los estudiantes para enfrentar desafíos como el de la pregunta 61.
Un Llamado a Fortalecer el Pensamiento Matemático
El desafío planteado por la pregunta 61 de la PAES de Matemáticas M1 no solo resalta la dificultad de ciertas secciones de la prueba, sino que también pone de manifiesto la necesidad de fortalecer el razonamiento y la interpretación en los estudiantes de matemáticas. Es crucial que sigamos fomentando una enseñanza que prepare a los estudiantes para enfrentar problemas complejos con una mentalidad crítica y analítica, adaptada a los requerimientos de una prueba como la PAES.
Como profesores, debemos estar conscientes de que problemas como estos no solo miden el conocimiento adquirido, sino también la capacidad de los estudiantes para abordar situaciones nuevas y complejas con creatividad y lógica matemática. En un articulo anterior abordé algunas estrategias para potenciar el proceso de enseñanza de matemáticas, propuse un ejemplo relacionado con el rol rol de la IA en el aprendizaje.
Atte. Patricio Figueroa M – Profesor de Matemáticas







